20 Soal Eksponen dan Deret Aritmatika

 1. Tentukan penyelesaian dari persamaan ekponensial berikut ini  22x-7 = 81-x

Jawab:
Pertama-tama menyamakan basis pada kedua ruas [ruas kanan dan ruas kiri] seperti berikut:
22x-7 = 81-x
22x-7 = (23)1-x
22x-7 = 23-3x
Nah karena basismya telah sama, maka dengan mudah kita dapat menentukan nilai x-nya seperti berikut ini.
2x – 7 = 3 – 3x
5x = 10
x = 2
Sehingga kita peroleh x = 2

2. Tentukan nilai x yang memenuhi persamaan eksponensial berikut

3ˣ⁺²+3ˣ=10
Jawab:
3ˣ⁺²+3ˣ=10
3ˣ(3²+1)=10

3ˣ(10)=10
3ˣ = 1
3ˣ=3⁰
x=0

3. Tentukan nilai x dari persamaan 3⁵ˣ⁻¹ – 27ˣ⁺³ = 0

Jawab:
3⁵ˣ⁻¹ – 27ˣ⁺³ = 0
3⁵ˣ⁻¹ = (3³)ˣ⁺³
3⁵ˣ⁻¹ = 3³ˣ⁺⁹
5x-1 = 3x + 9
   2x = 10
     x = 5

4. (6a3)2 : 2a4 = …

Penyelesaian:

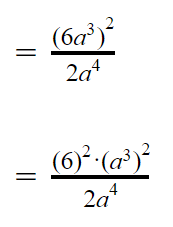
Di sini kamu lihat ya kalo (a3)2 itu merupakan bilangan berpangkat yang dipangkatkan lagi. Jadi, berdasarkan sifat eksponen poin 3, kita bisa kalikan pangkatnya.

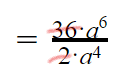
Kemudian, pangkat 6 bisa dikurangi dengan pangkat 4 karena merupakan operasi pembagian dengan basis yang sama. Jadi, jawabannya:

= 18a2                        (Jawaban)

5. Nilai $x$ yang memenuhi $\frac{2^x}{4^{x+2}}=16\cdot 4^x$ adalah$\cdots$

$\begin{array}{cc}\frac{2^x}{4^{x+2}}& =16\cdot 4^x\\ 2^x& =2^4\cdot 4^x\cdot 4^{x+2}\\ 2^x& =2^4\cdot 2^{2x}\cdot 2^{2x+4}\\ 2^x& =2^{4+2x+2x+4}\\ 2^x& =2^{4x+8}\\ x& =4x+8\\ -3x& =8\\ x& =-\frac{8}{3}\end{array}$

$\therefore$ Pilihan yang sesuai adalah $\left(B\right)-\frac{8}{3}$

6. Suatu bentuk deret aritmetika adalah 5, 15, 25, 35, …. Berapakah jumlah 10 suku pertama dari deret aritmetika tersebut?

Diketahui:

n = 10

U1 = a = 5

b = 15 – 5 = 25 – 15 = 10

Jawaban:

Sn = (2a + (n-1) b )

S10 = ( 2. 5 + (10 -1) 10)

= 5 ( 10 + 9.10)

= 5 x 100 = 500

Jadi, jumlah S10 dalam deret aritmetika tersebut, yakni 500.

7. Tentukan jumlah 20 suku pertama deret  3+7+11+...

Jawab:

Mencari beda dengan mengurangi suku setelah dengan duku sebelumnya dan dapat dituliskan sebagai berikut

𝑏 = 𝑈𝑛 − 𝑈𝑛−1

𝑏 = 𝑈2 − 𝑈1

𝑏 = 7 − 3

𝑏 = 4

Selanjutnya substitusi 𝑏 = 4 untuk mencari 𝑆20

Sn = ½ n (2a + (n - 1)b )

Sn = ½ . 20 (2 . 3 + (20 - 1)4 )

Sn = 10 (6 + 19 . 4 ) Sn = 10 (6 + 76)

Sn = 10 (82)

Sn = 820

Jadi, jumlah 20 suku pertama adalah 820

8. Suatu deret aritmetika dengan S12 = 150 dan S11 = 100, tentukan U12 !

Jawab:

Karena yang diketahui 𝑆12 dan 𝑆11 maka untuk mencari 𝑈𝑛 kita bisa gunakan rumus berikut :

𝑈𝑛 = 𝑆𝑛 − 𝑆𝑛−1

Un = Sn - Sn-1

U12 = S12 - S11

= 150 - 100

= 50

Jadi, nilai dari 𝑈12 adalah 50

9. Jumlah n pada suku pertama di dalam deret aritmatika adalah Sn = (5n – 19). Hitung perbedaan pada deret tersebut.

Jawab:

S1 = 1/2 (5(1) -19) = -7

S1 = U1 didefinisikan sebagai a yang termasuk suku pertama di dalam deret

S2 = 2/2 (5 × 2 – 19) = -9

S2 = U1 + U2 = a + (a + b)

S2 = -7 + (-7 + b) = -9

b = -9 + 14 = 5

10. Dalam suatu deret aritmatika, diketahui bahwa suku tengah dari deret tersebut ialah 32. Jika total n pada suku pertama adalah 672, Berapakah banyak suku yang ada pada deret tersebut?

Jawab:

ut = 1/2 (a + un) = 32

a + Un = 32 (2)

a + Un = 64

Sn = n/2 (a + Un)

672 = n/2 (64)

672 = n (32)

21 = n

11. Soal: Tentukan penyelesaian dari persamaan ekponensial berikut ini  22x-7 = 81-x

Jawab:

22x-7 = 81-x

22x-7 = (23)1-x

22x-7 = 23-3x

Nahhhh karena basismya telah sama, maka dengan mudah kita dapat menentukan nilai x-nya seperti berikut ini.

2x – 7 = 3 – 3x

5x = 10

x = 2

Sehingga kita peroleh x = 2

12. Soal: Tentukan nilai x yang memenuhi persamaan eksponensial berikut

3ˣ⁺²+3ˣ=10

Jawab:

3ˣ⁺²+3ˣ=10

3ˣ(3²+1)=10

3ˣ(10)=10

3ˣ = 1

3ˣ=3⁰

x=0

13. Soal: Tentukan himpunan penyelesaian dari :

9 x²+x = 27 x²-1 

Jawab: 

9 x²+x = 27 x²-1

3 2(x²+x) = 3 3(x²-1) 

2 (x2+x) = 3 (x2-1)

2x2 + 2x = 3x2 – 3

x2 – 2x – 3 = 0

(x – 3) (x + 1) = 0 

x = 3     atau   x = -1

Jadi himpunan penyelesaiannya adalah { -1,3 }

14. Soal: Tentukan nilai x yang memenuhi persamaan eksponensial berikut.

25 x+2 = (0,2) 1-x

Jawab

 

25 x+2 = (0,2) 1-x 

52(x+2) = 5 -1(1-x)

2x + 4 = -1 + x

2x – x = -1 – 4

x         = -5

Jadi nilai x yang diperoleh yaitu  -5

15. Berapa hasil x dari 3^x + 2 = 9^x - 2?

Jawaban:

3^x + 2 = 9^x - 2

3^x + 2 = 3^2^x + 2

x + 2 = 2x – 4

x = 6

16. Tentukan penyelesaian dari persamaan ekponensial berikut ini  22x-7 = 81-x

Jawab:

Pertama-tama yang perlu Gengs lakukan yaitu menyamakan basis pada kedua ruas [ruas kanan dan ruas kiri] seperti berikut:

22x-7 = 81-x

22x-7 = (23)1-x

22x-7 = 23-3x

Nahhhh karena basismya telah sama, maka dengan mudah kita dapat menentukan nilai x-nya seperti berikut ini.

2x – 7 = 3 – 3x

5x = 10

x = 2

Sehingga kita peroleh x = 2

17. Tentukan nilai x dari persamaan 3⁵ˣ⁻¹ – 27ˣ⁺³ = 0

Jawab:

3⁵ˣ⁻¹ – 27ˣ⁺³ = 0

3⁵ˣ⁻¹ = (3³)ˣ⁺³

3⁵ˣ⁻¹ = 3³ˣ⁺⁹

5x-1 = 3x + 9

   2x = 10

x = 5

 18. Tentukan nilai x yang memenuhi persamaan eksponensial berikut

3ˣ⁺²+3ˣ=10

Jawab:

3ˣ⁺²+3ˣ=10

3ˣ(3²+1)=10

3ˣ(10)=10

3ˣ = 1

3ˣ=3⁰

x=0

19. Akar-akar persamaan 2.3⁴ˣ – 20.3²ˣ + 18 = 0$ adalah x₁ dan x₂. Nilai x₁ + x₂ adalah

Jawab:

Dengan menggunakan sifat-sifat persamaan eksponen, maka:

2.3⁴ˣ – 20.3²ˣ + 18 = 0

(3²ˣ) – 10.3²ˣ + 9 = 0

(3²ˣ – 9)(3²ˣ – 1) = 0

3²ˣ = 9 atau 3²ˣ = 1

3²ˣ = 3² atau 3²ˣ = 3⁰

2x = 2 atau 2x = 0

x = 1 atau x = 0

Jadi x₁ + x ₂ = 1 + 0

20. Diketahui nilai dari persamaan 2y + 2-y = 5. Tentukan berapakah nilai dari persamaan eksponensial berikut 22y + 2-2y

Pembahasan:

22y + 2-2y

= (2y)² + (2-y)²

= (2y + 2-y)² - 2 (2y . 2-y)

= (5)² - 2 (20)

= 25 – 2 (1)

= 25 – 2

= 23